검색결과 리스트
글
本文对K-Means聚类分析进行了详细的讲解,包括对理论的简略说明和详细的SPSS操作过程,以及部分参考文献供大家参考学习。
目录1. 什么是聚类分析2. K-Means步骤3. 初始中心点怎么确定4. K值怎么确定5. 理论小结6. SPSS操作方法7. 参考论文下载
1. 什么是聚类分析
只有数据,无明确答案,即训练集没有标注目标变量,由计算机自己找出规律,把有相似属性的样本放在一组,每个小组也称为簇或集团(cluster)。
其实,最早的聚类分析是在考古分类、昆虫分类研究中发展起来的,目的是找到隐藏于数据中客观存在的“自然小类”,“自然小类”具有类内结构相似、类间结构差异显著的特点,通过刻画“自然小类”可以发现数据中的规律、揭示数据的内在结构。
如何高效的使用聚类分析,主要体现在聚类变量的选择和对于聚类结果的解读。比如要对于现有的客户分群,那么就要根据最终分群的目的选择不同的变量来分群,这就需要专家经验或者基础理论的支持。如果要优化客户服务的渠道,那么就应选择与渠道相关的数据;如果要推广一个新产品,那就应该选用用户目前的使用行为的数据来归类用户的兴趣,单靠算法是无法做到这一点的。
欠缺经验的分析人员和经验丰富的分析人员对于结果的解读会有很大差异。当然,不光是聚类分析,所有的分析都不能仅仅依赖统计学家或者数据工程师,其实这也给了我们很大的诠释空间。
2. K-Means基本原理
K-Means聚类步骤是一个循环迭代的算法,非常简单易懂:
-
假定我们要对N个样本观测做聚类,要求聚为K类,首先选择K个点作为初始中心点;
-
接下来,按照距离初始中心点最小的原则,把所有观测分到各中心点所在的类中;
-
每类中有若干个观测,计算K个类中所有样本点的均值,作为第二次迭代的K个中心点;
-
然后根据这个中心重复第2、3步,直到收敛(中心点不再改变或达到指定的迭代次数),聚类过程结束。
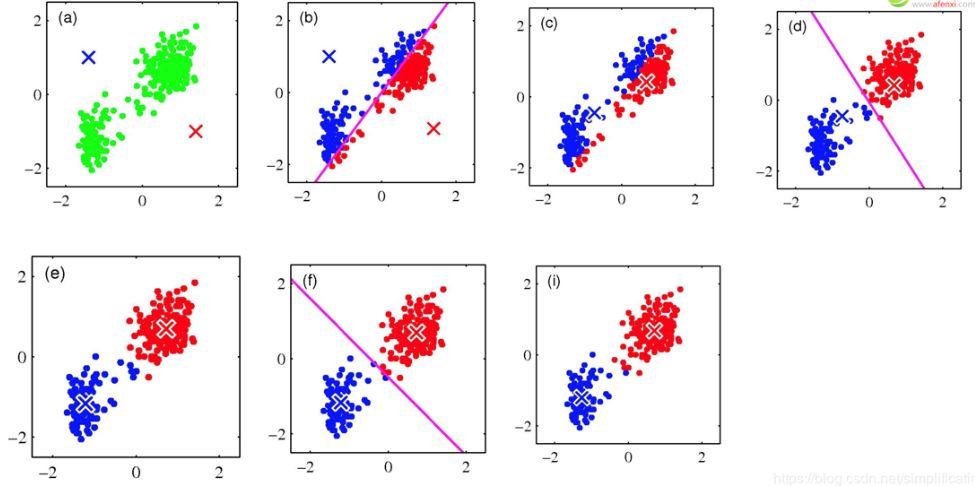
以二维平面中的点为例,用图片展示K=2时的迭代过程:
-
现在我们要将图(a)中的n个绿色点聚为2类,先随机选择蓝叉和红叉分别作为初始中心点;
-
分别计算所有点到初始蓝叉和初始红叉的距离,距离蓝叉更近就涂为蓝色,距离红叉更近就涂为红色,遍历所有点,直到全部都染色完成,如图(b);
-
现在我们不管初始蓝叉和初始红叉了,对于已染色的红色点计算其红色中心,蓝色点亦然,得到第二次迭代的中心,如图(c );
-
重复第2、3步,直到收敛,聚类过程结束。
3. 初始中心点怎么确定
在k-means算法步骤中,本质目标就是实现同一个簇中的样本差异小,即最小化SSE。在分析中,有两个地方降低了SSE(误差项平方和):
把样本点分到最近邻的簇中,这样会降低SSE的值;重新优化聚类中心点,进一步的减小了SSE。
这样的重复迭代、不断优化,会找到局部最优解(局部最小的SSE),如果想要找到全局最优解需要找到合理的初始聚类中心。
那合理的初始中心怎么选?
方法有很多,譬如先随便选个点作为第1个初始中心C1,接下来计算所有样本点与C1的距离,距离最大的被选为下一个中心C2,直到选完K个中心。这个算法叫做K-Means++,可以理解为 K-Means的改进版,它可以能有效地解决初始中心的选取问题,但无法解决离群点问题。
总的来说,最好解决办法还是多尝试几次,即多设置几个不同的初始点,从中选最优,也就是具有最小SSE值的那组作为最终聚类。
4. K值怎么确定
这个其实是大家最关心的地方吧。
理论上来说,K设置得越大,样本划分得就越细,每个簇的聚合程度就越高,误差平方和SSE自然就越小。但是无限大的设置K值,会使集团数量过多,分析起来更为复杂,无法进行实际应用,违背了聚类分析的初衷。所以不能单纯像选择初始点那样,用不同的K来做尝试,选择SSE最小的聚类结果对应的K值,因为这样选出来的肯定是你尝试的那些K值中最大的那个。
确定K值的一个主流方法叫“手肘法”。
如果我们拿到的样本,客观存在J个“自然小类”,这些真实存在的小类是隐藏于数据中的。三维以下的数据我们还能画图肉眼分辨一下J的大概数目,更高维的就不能直观地看到了,我们只能从一个比较小的K,譬如K=2开始尝试,去逼近这个真实值J。
-
当K小于样本真实簇数J时,K每增大一个单位,就会大幅增加每个簇的聚合程度,这时SSE的下降幅度会很大;
-
当K接近J时,再增加K所得到的聚合程度回报会迅速变小,SSE的下降幅度也会减小;
-
随着K的继续增大,SSE的变化会趋于平缓。
例如下图,真实的J我们事先不知道,那么从K=2开始尝试,发现K=3时,SSE大幅下降,K=4时,SSE下降幅度稍微小了点,K=5时,下降幅度急速缩水,再后面就越来越平缓。所以我们认为J应该为4,因此可以将K设定为4。
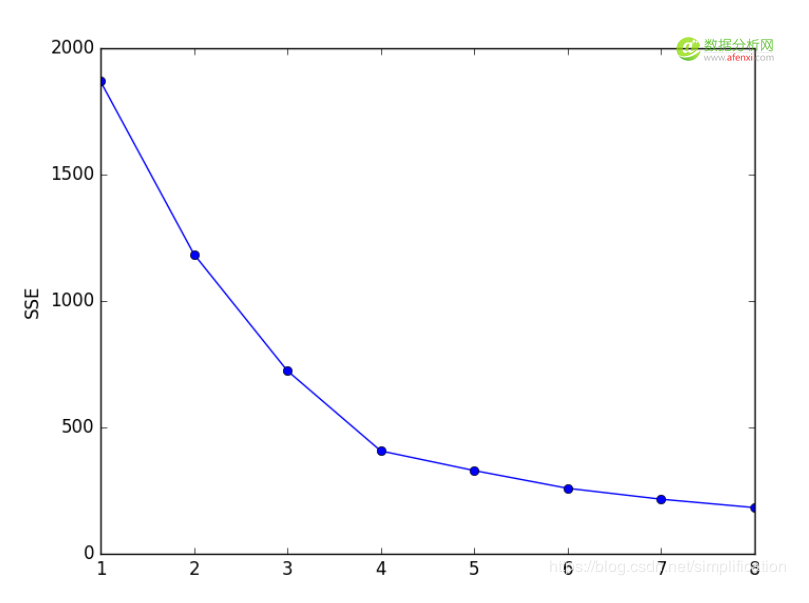
叫“手肘法”可以说很形象了,因为SSE和K的关系图就像是手肘的形状,而肘部对应的K值就被认为是数据的真实聚类数。
当然还有其他设定K值的方法,这里不赘述,总的来说还是要结合自身经验多做尝试,要知道没有一个方法是完美的。
5. 理论小结
K-Means优点在于原理简单,容易实现,聚类效果好。
当然,也有一些缺点:比如K值、初始点的选取不好确定;得到的结果只是局部最优;受离群值影响大等等。
每个算法都有自己的特点,所以要多学习,掌握不同算法的逻辑、作用、应用场景和优缺点。这样的话,在需要解决实际问题时,就容易结合自身经验,选出最合适的算法模型来达到自己的目标。
6. SPSS操作方法
1. 准备好数据,在菜单栏上执行:analyse--classify--k-means cluster,打开k平均数对话框。

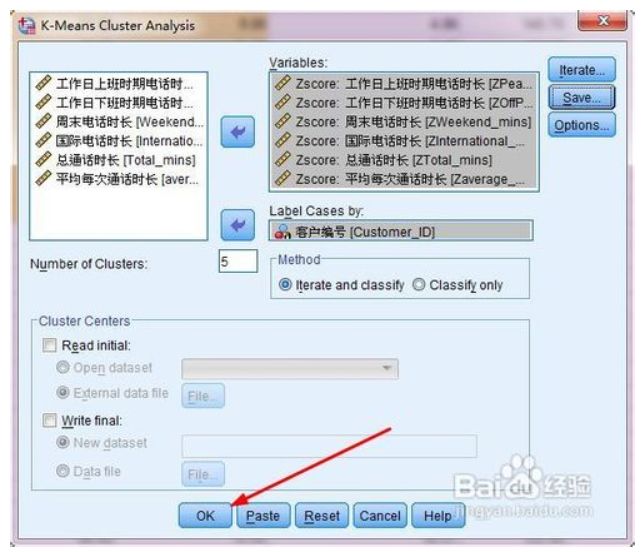
2. 将聚类用到的指标变量放入variables,将客户的编码(ID)放到label cases by当中,把客户编号作为case的标签。

3. 接着要设置聚类的类别数目,如图所示,这个数目不是随便给的,他有两个来源:要么是你根据工作经验,认为数据分为几类是最合理的;要么是你有前人的研究证明分为几类。
当然,这个数值是需要多尝试几次的,选取结果最佳的数值就好了。

4. 在主对话框中,点击iterate按钮,打开迭代对话框。

5. 将最大迭代次数设置为100,下图你看到的默认的迭代次数为10,但是数据量越大,迭代次数就应该越多,所以我们设置为100.点击continue按钮,返回到主对话框。
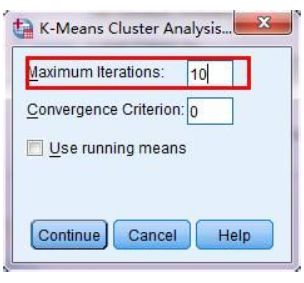
6. 点击save按钮,因为我们想要保存分类的结果,并将结果保存到一个变量当中。
7. 打开一个自对话框,勾选cluster membership(将分组后的组号另存为一个新的变数),点击continue返回到主对话框。

8. 点击ok,开始运行数据,并输出数据结果
9. 我们看到的第一个表格叫做初始聚类中心,它列出每一个类别初始的中心点,这些中心点都是spss自动生成的。因为case的顺序会影响到中心点的位置,所以我们需要让case的顺序是随机的,有必要的时候要进行随机化处理。
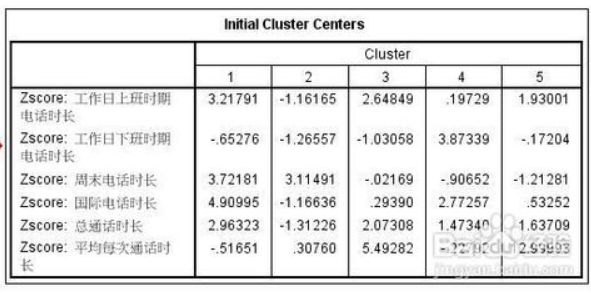
10. 下面的两个表格是迭代过程表,你可以看到每一次迭代中心点的变化值,当中心点的变化小于初始类别中心最小距离的2%的时候,迭代就停止了,你看到的第二幅图在迭代35次以后就停止了迭代。换句话说,这个数据最多只能分成35个组。

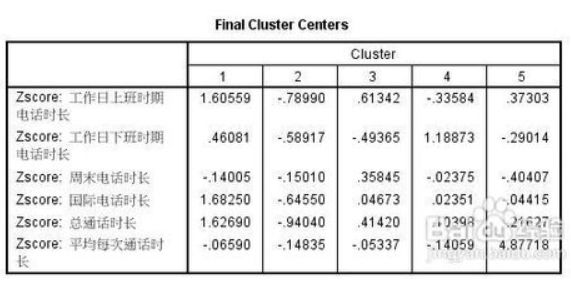
11. 下面这个表格叫做最终聚类中心,也就是各个类别在各个变量上的平均值,它可以帮助我们根据变量的平均值来给分类赋予实际的意义。
比如说,第一个集团,工作日上班时期电话时长,国际电话时长,总通话时长均为最高值,这些就是集团1的共同特性,因此聚类分析将具有这些特性的标本分成为一组。
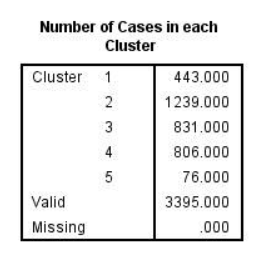
12. 最后的表格叫做各个类别case数,你可以读出在每一个类别中有多少case。
13. 回到数据界面,在最后会生成一个新的变数——组别号码,用来区分当前的标本分别属于哪个群组(cluster)。

7. 参考论文下载
这里有几篇比较好的,使用K-Means聚类分析方法的论文,写论文的时候不妨多参考一下,仿照人家的写法,会少走很多弯路。
下载链接: https://pan.baidu.com/s/1PUkviWXW3O1PP2xic5fF7A
提取码: hjyz
-
임애령, 이형룡(2014). 소비가치 세분화에 의한 선호관광활동 비교 -내일로 자유 열차티켓 이용자를 중심으로, 관광학연구, 38(1): 33-53.
-
차문경, 이희태(2018). 온·오프라인 사회적 자본에 대한 이용자 특성의 영향: 소비특성과 온라인네트워크 사용특성을 중심으로 한 군집 및 판별분석, 大韓經營學會誌, 31(5), 963-980.
-
심주원, 정진선(2018). 군집분석을 활용한 청소년의 자기가치수반성 유형분류와 영향요인 탐색, 상담학연구, 19(5), 297-315.
本文来自作者的总结和互联网知识,只要参考内容如下
-
SPSS教程学习笔记5:kmeans聚类分析在市场细分中的应用,http://www.datasoldier.net/archives/391
-
spss中k-means聚类的操作方法,https://jingyan.baidu.com/article/4665065867a402f549e5f8ed.html
-
数据分析网,用人话讲明白kmeans聚类算法,https://www.afenxi.com/68641.html


数据分析
毕业论文的数据分析搞不定吗?数据分析、结果说明、一对一讲解一站式服务
-
SPSS, AMOS软件的数据分析
-
毕业论文,期末课题数据分析
-
数据收集
精彩推荐
'统计分析' 카테고리의 다른 글
| 数据分析的常见问题合集之一 (0) | 2019.12.11 |
|---|---|
| 理解 t 检验与 F 检验的区别 (0) | 2019.11.25 |
| 显著性(p)到底是什么? (0) | 2019.07.23 |
| SPSS数据分析:多重响应分析,问卷调查中多选题的分析方法 (0) | 2019.06.24 |
| 【转】 玩转量表:量表设计与分析实战 (0) | 2019.05.27 |


RECENT COMMENT